Yakko, Wakko và Dot chơi xúc xắc. Yakko ném xúc xắc và nhận được điểm Y, điểm Wakko là W. Đến lượt của Dot. Nhưng cô không vội. Dot muốn biết chắc chắn cơ hội chiến thắng của cô là bao nhiêu. Được biết, Yakko và Wakko là những quý ông đích thực, đó là lý do tại sao nếu họ có cùng số điểm với Dot, họ sẽ để Dot giành chiến thắng.

Input: Dòng duy nhất của tệp đầu vào chứa hai số tự nhiên Y và W - kết quả của các lần tung xung xắc của Yakko và Wakko.

Output: Đưa ra xác suất cần thiết dưới dạng phân số không thể thay đổi theo định dạng "A/B", trong đó A - tử số và B - mẫu số. Nếu xác suất yêu cầu bằng 0, xuất ra "0/1". Nếu xác suất yêu cầu bằng 1, xuất ra "1/1".

Ví dụ:

Input:

4 2

Ouput:

1/2

Gần đây Anton tìm thấy một hộp có chữ số trong phòng của mình. Có k2 chữ số 2, k3 chữ số 3, k5 chữ số 5 và k6 chữ số 6. Số nguyên yêu thích của Anton là 32 và 256. Anh quyết định soạn số nguyên này từ các chữ số anh có. Anh ta muốn làm cho tổng của các số nguyên này càng lớn càng tốt. Giúp anh ta giải quyết nhiệm vụ này!

Mỗi chữ số có thể được sử dụng không quá một lần, tức là các số nguyên tổng hợp nên chứa không quá k2 chữ số 2, k3 chữ số 3, v.v. Tất nhiên, các chữ số không sử dụng không được tính vào tổng.

Input: Dòng duy nhất của đầu vào chứa bốn số nguyên k2, k3, k5 và k6 - số chữ số 2, 3, 5 và 6 tương ứng (0 ≤ k2, k3, k5, k6 <=5.10^6).

Output: In một số nguyên - tổng số tối đa có thể có của các số nguyên yêu thích của Anton có thể được tạo bằng các chữ số từ hộp.

Ví dụ:

Input:

5 1 3 4

Output:

800

Một người lính muốn mua w quả chuối trong cửa hàng. Anh ta phải trả k đô la cho quả chuối đầu tiên, 2k đô la cho quả thứ hai và cứ thế (nói cách khác, anh ta phải trả i * k đô la cho quả chuối thứ i). Anh ta có n đô la. Anh ta phải vay bao nhiêu đô la từ người bạn lính của mình để mua chuối?

Input: Dòng đầu tiên chứa ba số nguyên dương k, n, w (1 ≤ k, w ≤1000, 0 ≤n≤109), chi phí của quả chuối đầu tiên, số đô la ban đầu mà người lính có và số chuối anh ta muốn.

Output: Xuất ra một số nguyên - số đô la mà người lính phải vay từ bạn của mình. Nếu anh ta không phải vay tiền, đầu ra là 0.

Ví dụ:

Input:

3 17 4

Output:

13

Hôm nay Patrick chờ đợi một chuyến thăm từ người bạn SpPal của mình. Để chuẩn bị cho chuyến thăm, Patrick cần mua một số quà tặng ở hai cửa hàng gần nhà. Có một con đường dài d1 mét giữa nhà anh ta và cửa hàng đầu tiên và một con đường dài d2 mét giữa nhà anh ta và cửa hàng thứ hai. Ngoài ra, có một con đường dài d3 kết nối trực tiếp hai cửa hàng này với nhau. Giúp Patrick tính toán khoảng cách tối thiểu mà anh ta cần đi bộ để đến cả hai cửa hàng và trở về nhà. Patrick luôn bắt đầu tại nhà của mình. Anh ta nên ghé thăm cả hai cửa hàng chỉ di chuyển dọc theo ba con đường hiện có và trở về nhà của anh ta. Anh ta không ngại ghé thăm cùng một cửa hàng hoặc đi qua cùng một con đường nhiều lần. Mục tiêu duy nhất là giảm thiểu tổng quãng đường đã đi.

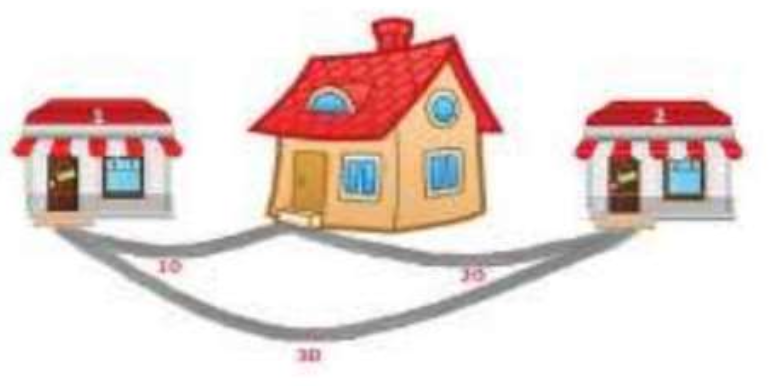
Input: Dòng đầu tiên của đầu vào chứa ba số nguyên d1, d2, d3 (1 <=d1, d2, d3<= 10^8) - độ dài của các đường dẫn. d1 là chiều dài của con đường nối nhà Patrick và cửa hàng đầu tiên; d2 là chiều dài của con đường nối nhà Patrick và cửa hàng thứ hai; d3 là chiều dài của đường dẫn kết nối cả hai cửa hàng.

Output: In khoảng cách tối thiểu mà Patrick sẽ phải đi bộ để ghé thăm cả hai cửa hàng và trở về

Ví dụ:

Input:

10 20 30

Output:

60

Quảng trường Nhà hát ở thủ đô Berland có hình chữ nhật với kích thước n × m mét. Nhân dịp kỷ niệm thành phố, một quyết định đã được đưa ra để lát Quảng trường bằng những viên bằng đá granit vuông. Mỗi viên đá hình vuông có kích thước a × a. Số lượng viên đá ít nhất cần thiết để lát Quảng trường là bao nhiêu? Nó được phép che phủ bề mặt lớn hơn Quảng trường Nhà hát. Nó không được phép phá vỡ các viên đá. Các cạnh của viên đá phải song song với các cạnh của Quảng trường.

Input: Đầu vào chứa ba số nguyên dương trong dòng đầu tiên: n, m và a (1 ≤ n, m, a ≤ 10^9).

Output: Viết số lượng viên đá cần thiết để lát kín quảng trường.

Ví dụ:

Input:

6 6 4

Output:

4

Bạn được cung cấp một bảng hình chữ nhật có kích thước M × N hình vuông đơn vị. Ngoài ra, bạn được cung cấp một số lượng không giới hạn các mảnh domino tiêu chuẩn kích thước 2 × 1. Bạn được phép xoay các mảnh domino. Bạn được yêu cầu đặt càng nhiều domino càng tốt trên bảng để đáp ứng các điều kiện sau:

1. Mỗi domino hoàn toàn bao gồm hai hình vuông đơn vị.

2. Không có hai domino trùng nhau.

3. Mỗi domino nằm hoàn toàn bên trong bảng. Nó được phép chạm vào các cạnh của bảng.

Tìm số lượng domino tối đa thỏa mãn điều kiện trên.

Input: Trong một dòng duy nhất, bạn được cung cấp hai số nguyên M và N - kích thước bảng theo hình vuông (1 ≤ M ≤ N<= 16)

Output: Xuất ra một số - số lượng domino tối đa, có thể được đặt.

Ví dụ:

Input 01:

3 3

Output 01:

4

Input 02:

2 4

Output 02:

4

Cho biết diện tích của ba mặt có chung đỉnh của hình hộp chữ nhật, tính tổng độ dài 12 cạnh của hình hộp chữ nhật đó.

Input: 3 số nguyên dương không vượt quá 10^4 là diện tích của ba mặt có chung đỉnh.

Output: Tổng của tất cả các cạnh của hình hộp chữ nhật.

Ví dụ:

Input:

4 6 6

Output:

28