Tại ngân hàng có các mệnh giá băng 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000. Tổng số tiền cần đổi có giá trị bằng N. Hãy xác định xem có ít nhất bao nhiêu tờ tiền sau khi đổi tiền?

Dòng duy nhất chứa số nguyên N

Ràng buộc: 1<=N<=10^9

Đầu ra: In ra số tờ tiền tối thiểu

Input:

138

Output:

6

Trong một buổi học toán, giáo viên viết 2 số nguyên A và B và yêu cầu Tý thực hiện phép cộng. Tý không bao giờ tính toán sai nhưng thỉnh thoảng cậu ta chép các con số một cách không chính xác. Lỗi duy nhất của Tý là ghi nhầm '5' thành '6' hoặc ngược lại.

Cho hai số, A và B, tính tổng lớn nhất và nhỏ nhất mà Tý có thể nhận được nếu bị nhầm.

Input Format: 1 dòng duy nhất chứa 2 số A và B

Ràng buộc: ~1 \leq A \leq B \leq 10^6~

Input 01:

35 36

Output 01:

72 70

Input 02:

891 746

Output 02:

1637 1636

Cho mảng A gồm N phần tử, nhiệm vụ của bạn là sắp đặt lại vị trí các phần tử trong mảng và tính toán giá trị lớn nhất của biểu thức:

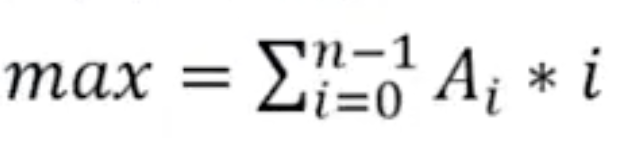
Đầu vào: Dòng 1 chứa số nguyên dương N; Dòng 2 chứa N số nguyên của mảng A[] viết cách nhau một dấu cách

Ràng buộc: 1<=N<=10^6; 1<=A[i]<=10^9;

Đầu ra: In ra kết quả của bài toán chia dư với 10^9 + 7

Input:

6
8 1 7 9 8 1

Output:

116

Cho mảng A[] gồm N số nguyên không âm và số K. Nhiệm vụ của bạn là hãy chia mảng A[] thành hai mảng con có kích cỡ K và N-K sao cho hiệu giữa tổng hai mảng con là lớn nhất. Ví dụ với mảng A[] = {8, 4, 5, 2, 10}, K=2 ta có kết quả là 17 vì mảng A[] được chia thành hai mảng {4, 2} và { 8, 5, 10} có hiệu của hai mảng con là 23-6=17 là lớn nhất.

Đầu vào: Dòng duy nhất chứa 2 số nguyên N và K; Dòng thứ 2 gồm N số của mảng A[]

Ràng buộc: 1<=K<=N<=10^6; 0<=A[i]<=10^9;

Đầu ra: In ra đáp án của bài toán

Input:

6 4
3 10 10 7 5 2

Output:

27

Cho mảng A[] gồm N số, hãy thực hiện các thao tác theo nguyên tắc dưới đây:

1. Ta chọn một mảng con sao cho phần tử ở giữa của mảng con cũng là phần tử ở giữa của mảng A[] (trong trường hợp N lẻ).

2. Đảo ngược mảng con đã chọn trong mảng A[]. Ta được phép chọn mảng con và phép đảo ngược mảng con bao nhiêu lần tùy ý.

Ví dụ với mảng A[] = (1, 6, 3, 4, 5, 2, 7} ta có câu trả lời là YES vì: ta chọn mảng con {3, 4, 5) và đảo ngược để nhận được mảng All=(1, 6, 5, 4, 3, 2, 7}, chọn tiếp mảng con {6, 5, 4, 3, 2} và đảo ngược ta nhận được mảng A[]=(1, 2, 3, 4, 5, 6, 7}.

Hãy cho biết ta có thể sắp xếp được mảng A[] bằng cách thực hiện các thao tác kể trên hay không?

Đầu vào:

Dòng 1 chứa số nguyên dương N là số lẻ.

Dòng 2 chứa N số nguyên của mảng A[]

Ràng buộc: 1 <= N <= 10^6; 0 <= A[i] <= 10^9

Đầu ra: In ra YES hoặc NO là đáp án của bài toán

Input 01:

5
1 4 3 2 5

Output 01:

YES

Input 02:

5
1 3 8 7 3

Output 02:

NO

Cho mảng A[], B[] đều có N phần tử. Nhiệm vụ cúa bạn là tìm giá trị lớn nhất của biểu thức P= A[0]B[0] + A[1]B[1] + ..+A[N-1]*B[N-1] bằng cách tráo đổi vị trí các phần tử của cả mảng A[] và B[].

Đầu vào: Dòng 1 chứa số nguyên dương N; Dòng 2 chứa N số nguyên của mảng A[]; Dòng 3 chứa N số nguyên của mảng B[]

Ràng buộc: 1 <= N＜= 10^5; 0 <= A[i], B[i] <= 10^6

Đầu ra: In ra đáp án của bài toán

Input:

7
9 4 5 3 9 4 10
9 5 3 1 10 1 5

Output:

270

Hoàng yêu thích các số may mắn. Ta biết rằng một số là số may mắn nếu biểu diễn thập phân của nó chỉ chứa các chữ số may mắn là 4 và 7. Ví dụ, các số 47, 744, 4 là số may mắn và 5, 17, 467 không phải. Hoàng muốn tìm số may mắn bé nhất có tổng các chữ số bằng n. Hãy giúp anh ấy.

Đầu vào: Dòng duy nhất chứa số nguyên dương n

Ràng buộc: 1<=n<=10^6;

Đầu ra: In ra đáp án của bài toán, nếu không tồn tại đáp án thì in ra -1

Input:

16

Output:

4444

Cho xâu kí tự chỉ bao gồm các kí tự in thường, hãy kiểm tra xem có thể sắp đặt lại các kí tự trong xâu sao cho không có 2 kí tự kề nhau nào giống nhau hay không?

Đầu vào: Dòng duy nhất chứa xâu S

Ràng buộc: 1<=len(S)<=10000;

Đầu ra: Nếu có thể sắp đặt lại xâu kí tự in ra YES, ngược lại in ra NO.

Input:

aqeaaqwq

Output:

YES

Cho hai số nguyên dương S và D, trong đó S là tổng các chữ số và D là số các chữ số của một số. Nhiệm vụ của bạn là tìm số nhỏ nhất thỏa mãn S và D?

Đầu vào: 1 dòng gồm 2 số S, D

Ràng buộc: 1<=S,D<=1000;

Đầu ra: In ra số nhỏ nhất có D chữ số và có tổng bằng S, nếu không tìm được đáp án thì in ra -1

Input:

12 8

Output:

10000029

Một phân số đơn vị nếu tử số của phân số đó là 1. Mọi phân số nguyên dương đều có thể biểu diễn thành tổng các phân số đơn vị. Ví dụ 2/3 = 1/2 + 1/6. Cho phân số nguyên dương P/Q bất kỳ, hãy biểu diễn phân số nguyên dương thành tổng phân số đơn vị với số hạng tử là ít nhất.

Đầu vào: 1 dòng duy nhất chứa 2 số P, Q

Ràng buộc: 1<=P,Q<=200

Đầu ra: Đưa ra đáp án trên 1 dòng

Input:

5 6

Output:

1/2 + 1/3

Cho dãy số A gồm N phần tử là các số nguyên. Hãy tính tích lớn nhất của 2 hoặc 3 phần tử trong dãy.

Đầu vào: Dòng đầu tiên là N; Dòng thứ 2 là N phần tử của mảng A

Ràng buộc: 1<=N<=1000; 0<=abs(A[i])<=10^6

Đầu ra: In ra tích lớn nhất của 2 hoặc 3 phần tử trong mảng

Input:

5
-9 4 3 -3 1

Output:

108

Cho số nguyên dương N, nhiệm vụ của bạn là kiểm tra xem có thể viết N = a * b * c hay không, trong đó a, b, c là 3 số nguyên dương lớn hơn hoặc bằng 2 khác nhau.

Đầu vào: Dòng duy nhất chứa số nguyên dương N

Ràng buộc: 2 <= N <= 10^9

Đầu ra: In ra YES nếu có thể biểu diễn N dưới dạng tích của 3 số, ngược lại in ra NO

Input 01:

11

Output 01:

NO

Input 02:

24

Output 02:

YES

Tí vào Tèo cùng chơi một trò chơi với xâu nhi phân S. Xâu nhị phân S chỉ bao gồm các kí tự 0 và 1. Ở mỗi bước đi, 2 bạn nhỏ có thể chọn 1 xâu con liên tiếp các kí tự giống nhau ở xâu S và xóa nó khỏi xâu S. Sau khi xóa 1 xâu thì 2 xâu bên trái và phải của xâu vừa xóa sẽ trở thành liền kề. Ban đầu Tí là người đi trước, sau đó 2 bạn lần lượt thực hiện bước đi của mình cho tới khi xâu S trở thành xâu rỗng. Bạn hãy xác định xem Tí có thể xóa tối đa bao nhiêu kí tự 1 biết rắng cả 2 bạn đều chơi tối ưu

Đầu vào: Dòng duy nhất chứa xâu S

Ràng buộc: 1<=len(S)<=100000;

Đầu ra: In ra số lượng số 1 tối đa mà Tí có thể xóa được

Input:

1000101110011111

Output:

6

Cô bé Anna đi mua sắm cùng mẹ và cô băn khoăn không biết làm thế nào để cải thiện chất lượng dịch vụ.

Có n người trong hàng đợi. Đối với mỗi người, chúng tôi biết thời gian cần thiết t để phục vụ anh ta. Một người sẽ thất vọng nếu thời gian anh ta chờ đợi nhiều hơn thời gian cần thiết để phục vụ anh ta. Thời gian một người chờ là tổng thời gian tất cả những người đứng trong hàng đợi trước mặt anh ta được phục vụ. Anna nghĩ răng nếu chúng ta hoán đổi một số người trong hàng đợi, thì chúng ta có thể giảm số người thất vọng.

Bạn hãy giúp Anna tìm ra con số tối đa mà những người không thất vọng có thể đạt được băng cách hoán đổi những người trong hàng đợi.

Đầu vào: Dòng đầu tiên chứa số N là số người trong hàng đợi; Dòng thứ 2 chứa N số là thời gian cần phục vụ của N người

Ràng buộc: 1<=N＜=10^5;1<=t<=10^9

Đầu ra: In ra đáp án của bài toán

Input:

7
4 3 17 4 5 14 20

Output:

3

Tí và Tèo chơi một trò chơi với xâu kí tự. Luật chơi như sau, ở mỗi lượt chơi 2 người có thể lựa chọn 1 trong 2 thao tác: 1. Hai người đi theo lượt, Tí là người đi trước, ở mỗi lượt đi 2 bạn nhỏ có thể lựa chọn 1 kí tự bất kỳ và xóa kí tự này khỏi xâu S. 2. Lấy xâu S sau đó sắp đặt lại các kí tự trong xâu sao cho nó là một xâu đối xứng thì người đó sẽ thắng. Biết rằng 2 bạn đều chơi tối ưu, bạn hãy xác định xem ai là người chiến thẳng ?

Đầu vào: Dòng duy nhất chứa xâu S

Ràng buộc: S chỉ bao gồm các kí tự in thường và có độ dài không quá 10000

Đầu ra: Nếu Tí thắng in ra 1, ngược lại nếu Tèo thẳng in ra 2

Input 01:

kpidpgb

Output 01:

1

Input 02:

safjagih

Output 02:

2

Sherlock Holmes nghi ngờ kẻ thù không đội trời chung của mình là Giáo sư Moriarty một lần nữa đang âm mưu điều gì đó ma quỷ. Bạn đồng hành của Sherlock, Tiến sĩ Watson, cho rằng Moriarty có thể phải chịu trách nhiệm về những vấn đề gần đây của MI6 với siêu máy tính The Beast của họ.

Ngay sau khi quyết tâm điều tra, Sherlock nhận được một bức thư từ Moriarty khoe khoang về việc đã lây nhiễm virus cho The Beast. Anh ta cũng cho Homes một manh mối đó là một số nguyên. Sherlock xác định chìa khóa để loại bỏ virus là tìm ra Số Decent lớn nhất có số chữ số đó.

Một số Decent có các thuộc tính sau:

1. Các chữ số của nó chỉ có thể là 3 và/hoặc 5.

2. Số lượng chữ số 3 chứa trong đó chia hết cho 5.

3. Số lượng chữ số 5 chứa trong đó chia hết cho 3.

4. Đó là con số lớn nhất xét theo chiều dài của nó.

Virus của Moriarty hiển thị một chiếc đồng hồ đang đếm ngược đến sự hủy diệt của The Beast và thời gian đang trôi qua rất nhanh. Nhiệm vụ của bạn là giúp Sherlock tìm ra chìa khóa trước khi The Beast bị tiêu diệt!

Ví dụ: Các số 55533333 và 555555 đều là số phù hợp vì đều là các số chỉ có 5 hoặc 3. Chúng là những giá trị lớn nhất cho những số có cùng độ dài và có khả năng số lượng chữ số 3 chia hết cho 5 và số lượng chữ số 5 chia hết cho 3

Đầu vào:

Dòng đầu tiên nhập vào số lượng test case

Từ dòng thứ 2 nhập vào số lượng chữ số trong một số Decent

Ràng buộc:

1 <= t <= 20

1 <= n <= 10^5

Đầu ra: In ra số thỏa mãn, nếu không tìm được thì in ra -1

Input:

4
1
3
5
11

Output:

-1
555
33333
55555533333