Di chuyển trong mê cung 1 (quay lui)
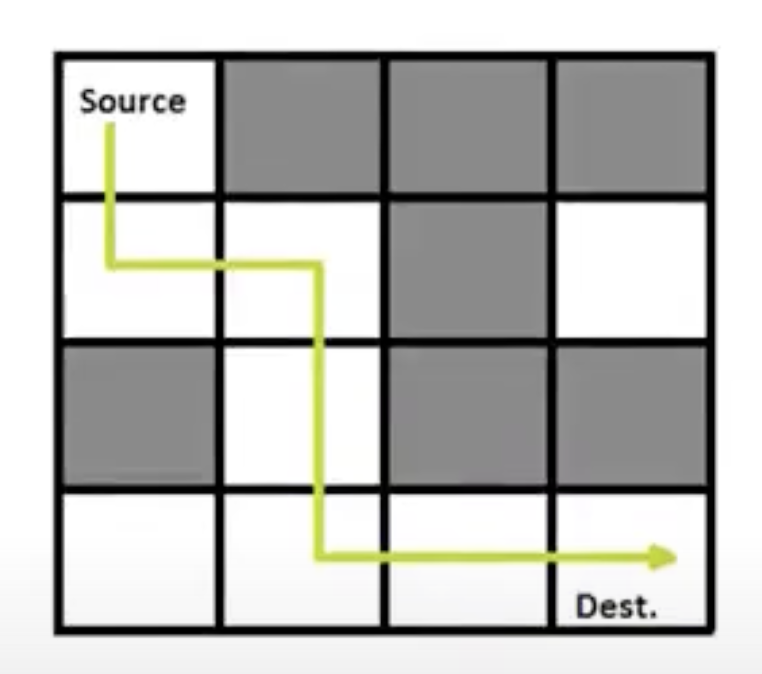
Xem dạng PDFCho một mê cung bao gồm các khối được biểu diễn như một ma trận nhị phân A[N][N]. Một con chuột đi từ ô đầu tiên góc trái (A[O][0]) đến ô cuối cùng góc phải (A[N-1][N-1]) theo nguyên tắc:
Down (D): Chuột được phép xuống dưới nếu ô dưới nó có giá trị 1.
Right (R): Chuột được phép sang phải dưới nều ô bên phải nó có giá trị 1.
Hãy đưa ra một hành trình của con chuột trên mê cung. Đưa ra -1 nếu chuột không thê đi đến đích.
Đầu vào:
Dòng đầu tiên đưa vào số lượng bộ test T.
Những dòng kế tiếp đưa vào các bộ test. Mỗi bộ test gồm hai phần: phần thứ nhất đưa vào số N là kích cỡ của mê cung; dòng tiếp theo đưa vào ma trận nhị phân A[N][N].
Ràng buộc: T, N, A thoa măn ràng buộc: 1 <= T <= 10; 2 <= N <= 10; O <= A[i][j] <= 1.
Đầu ra: Đưa ra các xâu ký tự được sắp xếp, trong đó mỗi xâu là một đường đi của con chuột trong mê cung. In ra đáp án theo thứ tự từ điển. Đưa ra -1 nếu chuột không đi được đến đích.
Input:
2
4
1 0 0 0
1 1 0 1
0 1 0 0
1 1 1 1
5
1 0 0 0 0
1 1 1 1 1
1 1 0 0 1
0 1 1 1 1
0 0 0 1 1
Output:
DRDDRR
DDRDRRDR DDRDRRRD DRDDRRDR DRDDRRRD DRRRRDDD
Bình luận
✅ Tóm tắt yêu cầu:
Bắt đầu từ ô (0,0), đến đích (N-1,N-1).
Chỉ đi xuống (D) nếu ô dưới là 1.
Chỉ đi sang phải (R) nếu ô bên phải là 1.
In tất cả các hành trình hợp lệ theo thứ tự từ điển.
Nếu không có đường đi → in -1.
💡 Chiến lược giải:
Dùng đệ quy (DFS) để tìm tất cả đường đi.
Với mỗi vị trí (i, j):
Nếu đi xuống (i+1, j) hợp lệ → đi tiếp, thêm D vào đường đi.
Nếu đi phải (i, j+1) hợp lệ → đi tiếp, thêm R vào đường đi.
Khi đến (N-1, N-1) → thêm đường đi vào danh sách.
Cuối cùng sắp xếp và in ra danh sách đường đi.